ポリゴン:コンピューターグラフィックスの立役者

ITの初心者
先生、『ポリゴン』ってコンピューターグラフィックスで使うって聞きましたけど、どういうものですか?

ITアドバイザー
そうだね。『ポリゴン』は簡単に言うと、コンピューターの中で立体的な絵を描くときに使う、小さな面のことだよ。三角形や四角形のような形をしていて、これをたくさん組み合わせて複雑な形を作るんだ。

ITの初心者
なるほど。でも、なんで小さな面をたくさん組み合わせる必要があるんですか?

ITアドバイザー
それはね、コンピューターは複雑な曲線をそのまま理解することが苦手なんだ。だから、小さな面をたくさん組み合わせることで、滑らかな曲線のように見せることができるんだよ。面の数が多ければ多いほど、より滑らかに、よりリアルな立体に見えるんだ。
polygonとは。
コンピューターで絵を描くときに、立体的な形を作るのに使われる『多角形』のことです。立体的な物の表面を三角形や四角形のような小さな形に分け、それぞれの場所、傾き、色、質感などを決めて、立体的に見せる方法です。
画面上の立体表現

絵を描くように、計算機で立体的な形を画面に表示するには、まずその形を決める必要があります。現実の世界では、物は滑らかな面でできているように見えますが、計算機でそれをそのまま再現するのは至難の業です。そこで、複雑な形をたくさんの小さな平面に分割することで、計算機は立体を扱いやすくしています。この小さな平面は、三角形や四角形などの多角形で、専門的にはポリゴンと呼ばれています。これらのポリゴンを組み合わせることで、滑らかな面を持つ立体を近似的に表現することができます。
例えば、球を考えてみましょう。最初は、角ばった多面体のような形になりますが、ポリゴンの数を増やすほど、より滑らかで球に近い形になります。数を増やすほど、より本物に近い表現が可能になりますが、同時に計算機の負担も増えます。ちょうど、たくさんの細かい部品で模型を作るようなもので、部品が多いほど精巧になりますが、作るのに時間も手間もかかります。
このように、立体を画面に表示する際には、ポリゴンが重要な役割を果たしています。例えば、テレビゲームや映画などでは、表現の豊かさと処理の速さのバランスを考えて、ポリゴンの数が調整されています。あまりにポリゴンが多いと、計算機に負担がかかりすぎて、動きが遅くなったり、止まったりしてしまうからです。逆に、ポリゴンが少なすぎると、形が荒く見えてしまいます。そのため、制作者は目的に合わせて最適なポリゴンの数を決める必要があります。
| 概念 | 説明 | 例 |
|---|---|---|
| 立体表現 | 計算機で立体を表示するには、多数の小さな平面(ポリゴン)に分割する。 | 球を多数のポリゴンで近似的に表現。 |
| ポリゴン | 三角形や四角形などの多角形。立体を構成する基本要素。 | – |
| ポリゴンの数と表現力 | ポリゴン数が多いほど滑らかでリアルな表現が可能になるが、計算機の負担も増える。 | ポリゴン数が多いほど球に近い形になる。 |
| ポリゴンの数と計算コスト | ポリゴン数が多いと計算コストが増加し、処理速度が低下する可能性がある。 | ゲームや映画でポリゴン数を調整して、表現力と処理速度のバランスをとる。 |
| 最適なポリゴン数 | 表現の豊かさと処理速度のバランスを考えて決定する必要がある。 | – |
ポリゴンの種類

図形を表現する際に、多角形は基本的な要素となります。多角形には、頂点の数によって様々な種類が存在します。例えば、三つの頂点を持つものは三角形、四つの頂点を持つものは四角形、五つの頂点を持つものは五角形と呼ばれます。これらの多角形の中でも、コンピューターグラフィックスの世界では、三角形と四角形が特に重要な役割を担っています。
三角形は、常に一つの平面上に存在するという特性を持っています。この特性により、三角形を扱う計算は比較的単純になり、結果として描画処理の高速化に繋がります。また、どんなに複雑な形をした多角形でも、複数の三角形を組み合わせることで表現することが可能です。このため、三角形はコンピューターグラフィックスにおける基本的な構成要素として広く利用されています。
四角形も、もし常に一つの平面上に存在することが保証されているならば、立体を効率的に表現するための優れた手段となります。四角形は、面としての情報を持つため、立体を構成する際に三角形よりも少ない数で表現できる場合があり、処理の効率化に貢献します。
しかし、五角形以上の多角形になると、必ずしも一つの平面上に存在するとは限りません。このような多角形を扱う場合、複雑な計算が必要となり、処理速度の低下を招く可能性があります。そのため、コンピューターグラフィックスでは、五角形以上の多角形を直接扱うことはあまりなく、多くの場合、三角形または四角形を組み合わせて複雑な形状を表現しています。このように、三角形と四角形は、コンピューターグラフィックスにおいて、処理の効率化と表現力の両立を図る上で重要な役割を果たしているのです。
| 頂点数 | 多角形の種類 | コンピューターグラフィックスでの役割 | 平面性 | 備考 |
|---|---|---|---|---|
| 3 | 三角形 | 基本的な構成要素。描画処理の高速化。 | 常に平面 | どんな多角形も三角形の組み合わせで表現可能 |
| 4 | 四角形 | 立体を効率的に表現。処理の効率化。 | 平面の場合が多い | 面としての情報を持つため、三角形より少ない数で立体を表現できる場合がある |
| 5以上 | 五角形以上 | あまり直接扱われない。三角形や四角形で代用。 | 平面とは限らない | 複雑な計算が必要となり、処理速度が低下する可能性がある |
ポリゴンの構成要素

多角形は、いくつかの要素が組み合わさってできています。まず、多角形の角にあたる点を頂点といいます。この頂点は、三次元空間上のどこに存在するかを示す座標によって位置が定められます。次に、二つの頂点を結ぶ線を辺といいます。そして、複数の辺で囲まれた平面を面といいます。
これらの要素に、色や質感、透明度といった情報を加えることで、より現実に近い表現ができるようになります。例えば、物体の表面の材質を表現するには、光沢や反射率、表面の粗さなどを細かく設定します。また、木目や金属の質感などを表現するために、模様を描いた画像を多角形の表面に貼り付けることもあります。このような画像を模様と呼びます。
これらの情報は、多角形一つ一つに設定できます。例えば、立方体であれば、六つの面それぞれに異なる色や模様を設定できます。これにより、複雑な形や模様を持つ立体を表現することが可能になります。例えば、レンガの壁を表現する場合、一つ一つのレンガに異なる色を設定することで、よりリアルな壁を表現できます。また、模様を使うことで、キャラクターの服に模様を描いたり、建物の壁にレンガの模様を表現したりすることができます。
このように、頂点、辺、面といった基本的な要素に加え、色、質感、透明度、模様といった情報を組み合わせることで、コンピューターグラフィックスで様々な立体を表現することができるのです。
| 要素 | 説明 | 追加情報 |
|---|---|---|
| 頂点 | 多角形の角にあたる点 | 座標によって位置が定まる |
| 辺 | 二つの頂点を結ぶ線 | |
| 面 | 複数の辺で囲まれた平面 | |
| 追加情報 | 色、質感、透明度、模様 | 多角形一つ一つに設定可能 例:光沢、反射率、表面の粗さ、木目、金属の質感など |
ポリゴンの役割

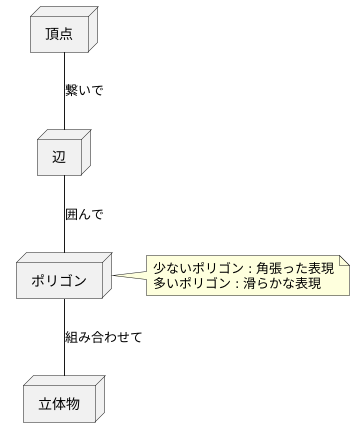
絵を描く時、点を打って線を引き、その線で面を作るのと同じように、コンピューターで立体的な絵を描くにも、同じような手順が必要です。コンピューターの中で絵を描くには、まず点を打ちます。この点は頂点と呼ばれます。次に、この頂点を線で繋ぎます。この線を辺と言います。そして、複数の辺で囲まれた面を作ります。これが、まさにポリゴンと呼ばれるものです。
ポリゴンは、コンピューターの中で立体物を表現するための最も基本的な部品のようなものです。例えば、立方体を思い浮かべてみてください。立方体は、六つの正方形で囲まれています。コンピューターで立方体を描くには、六つのポリゴン、つまり正方形を使います。
ポリゴンをたくさん使うほど、滑らかで、より本物に近い表現をすることができます。例えば、球を考えてみてください。球を少ない数のポリゴンで表現しようとすると、角張った、多面体のような見た目になります。しかし、ポリゴンの数を増やせば増やすほど、より滑らかで、球らしい形に近づきます。
近年のコンピューターの性能向上は目覚ましく、扱えるポリゴンの数も飛躍的に増えました。以前はカクカクとした表現しかできなかったものが、今では非常に滑らかで、まるで写真のようにリアルな表現も可能になっています。ゲームや映画、アニメーションなどで、まるで現実世界のような映像を見ることができるのは、このポリゴン技術の進化のおかげです。
ポリゴンの技術は、娯楽だけでなく、様々な分野で応用されています。建物の設計や、医療現場での手術のシミュレーション、製品のデザインなど、様々な分野で、ポリゴンを使って立体物を表現し、活用しています。コンピューターの中で仮想世界を作り、様々なことを試したり、確かめたりすることができるのも、ポリゴン技術のおかげです。これからも、ポリゴン技術はますます進化し、私たちの生活をより豊かにしてくれるでしょう。
今後の展望

絵を描くための計算機の技術は、常に進歩を続けています。図形を描くための基本的な部品である多角形も、より綺麗に、より細かく表現できるようになっています。少ない部品の数で、高画質の映像を作ることができる技術や、多角形以外の図形の描き方も研究されています。
しかし、多角形は、その使いやすさと自由度の高さから、これからも絵を描くための計算機の技術で重要な役割を果たし続けるでしょう。より本物らしく、より豊かな表現ができる仮想世界を作るために、多角形を描く技術は進歩し続けていくと考えられます。
計算機の処理能力が向上するにつれて、とても細かい多角形を、時間をかけずに描くことができるようになります。この技術のおかげで、まるで本当にその場にいるかのような、より深い没入感を味わうことができるようになるでしょう。例えば、ゲームの世界では、キャラクターの服の細かいしわや、髪の毛の一本一本までリアルに表現されるようになるかもしれません。また、映画やアニメーションの世界でも、より自然で生き生きとした映像表現が可能になるでしょう。さらに、医療分野では、人体内部の構造をより精密に再現することで、手術のシミュレーションや診断の精度向上に役立つことが期待されます。建築分野では、建物の設計段階で、よりリアルな外観や内部の様子を確認できるようになり、設計の効率化や完成度の向上に貢献するでしょう。
このように、多角形を描く技術の進歩は、様々な分野で革新をもたらす可能性を秘めています。これからの技術の進歩に、大きな期待が寄せられています。
| 分野 | 多角形描画技術の進歩による効果 | 具体例 |
|---|---|---|
| ゲーム | よりリアルな表現 | キャラクターの服のしわ、髪の毛一本一本のリアルな表現 |
| 映画・アニメーション | より自然で生き生きとした映像表現 | – |
| 医療 | 手術のシミュレーション、診断の精度向上 | 人体内部の構造の精密な再現 |
| 建築 | 設計の効率化、完成度の向上 | 建物の外観や内部のリアルな確認 |
