計算の落とし穴:打ち切り誤差とその影響

ITの初心者
先生、「打ち切り誤差」って、どういう意味ですか?コンピューターの計算で何か誤差が出るって聞いたんですけど…

ITアドバイザー
いい質問だね!コンピューターは無限に計算し続けることはできないから、どこかで計算を打ち切らないといけないんだ。そのせいで生まれる誤差を「打ち切り誤差」って言うんだよ。

ITの初心者
なるほど…。例えば、どんな時に「打ち切り誤差」は起こるんですか?

ITアドバイザー
例えば、円周率の計算をする時を想像してみて。円周率は無限に数字が続くけど、コンピューターの計算能力には限界があるから、どこかで計算を打ち切らないといけないよね?その時に、本来の円周率との間に誤差が生まれるんだ。これが「打ち切り誤差」の一例だよ。
打ち切り誤差とは。
コンピューターを使った計算では、計算を繰り返せば繰り返すほど正確な答えに近づいていく計算方法があります。しかし、コンピューターの能力には限界があり、永遠に計算を続けることはできません。そのため、ある程度のところで計算を打ち切らなければならず、その際に正しい答えと計算結果との間にずれが生じてしまいます。このずれを「打ち切り誤差」といいます。
コンピューターにおける数値計算の限界

現代社会において、コンピューターは日常生活に欠かせない存在となっています。複雑な計算を瞬時に行うその能力は、我々の生活を大きく変えました。しかし、一見完璧に見えるコンピューターにも、乗り越えられない壁が存在します。それは、数値計算における誤差です。
コンピューターは、数字を扱う際に、無限の桁数を持つことができません。そのため、有限の桁数で表現できる範囲内の数値しか扱うことができません。この制約が、数値計算の誤差を生み出す根本原因となっています。
例えば、円周率のような無理数は、無限に続く小数で表されます。しかし、コンピューター内部では、限られた桁数でしか表現できません。そのため、どうしても真の値との間に誤差が生じてしまうのです。
この誤差は、一見すると非常に小さく、無視できるものに思えるかもしれません。しかし、複雑な計算を何度も繰り返すと、この小さな誤差が積み重なって、最終的には大きな誤差となってしまうことがあります。
特に、科学技術計算や金融取引など、高い精度が求められる分野では、この数値計算の誤差が深刻な問題を引き起こす可能性があります。そのため、コンピューターにおける数値計算の限界を正しく理解し、誤差を最小限に抑えるための対策を講じる必要があります。
| 項目 | 内容 |
|---|---|
| コンピューターの役割 | 現代社会において不可欠な存在 |
| コンピューターの能力 | 複雑な計算を瞬時に行う |
| コンピューターの限界 | 数値計算における誤差 |
| 誤差の原因 | コンピューターが扱える数値の桁数が有限であるため |
| 誤差の例 | 円周率のような無理数の計算 |
| 誤差の影響 | 複雑な計算を繰り返すと誤差が蓄積し、大きな誤差となる可能性 |
| 重要な分野 | 科学技術計算、金融取引など、高い精度が求められる分野 |
| 対策 | コンピューターの限界を理解し、誤差を最小限に抑える対策が必要 |
打ち切り誤差:無限を有限にするための代償

– 打ち切り誤差無限を有限にするための代償コンピューターは、一見、完璧な計算機のように思えます。膨大な量の計算を、人間には不可能な速度と正確さでこなしてくれるからです。しかし、デジタルの世界では、無限を扱うことはできません。そこで登場するのが「打ち切り誤差」という概念です。円周率を例に考えてみましょう。円周率は、円周の長さを直径で割った値であり、3.14159…と無限に続く小数です。しかし、コンピューターのメモリには限りがあるため、円周率のような無限小数をそのまま扱うことはできません。そこで、ある桁で計算を打ち切り、有限の桁数で表現することになります。この「打ち切り」こそが、誤差を生み出す原因となるのです。例えば、円周率を3.14と表現した場合、真の値との間にはわずかな差が生じます。この差が、打ち切り誤差です。打ち切り誤差は、計算結果にわずかな「ずれ」を生み出すだけでなく、計算を繰り返すと誤差が蓄積し、結果的に大きな影響を及ぼす可能性も孕んでいます。打ち切り誤差は、コンピューターで数値計算を行う上で避けることのできない問題です。しかし、その影響を最小限に抑えるための工夫も存在します。例えば、計算に用いる桁数を増やしたり、誤差の蓄積を抑えるアルゴリズムを採用したりすることで、より正確な結果を得ることが可能になります。コンピューターの有限性と、現実世界に存在する無限。この両者の間には、乗り越えなければならない壁が存在します。打ち切り誤差は、その壁を象徴する概念と言えるでしょう。
| 概念 | 説明 | 例 | 影響 | 対策 |
|---|---|---|---|---|
| 打ち切り誤差 | コンピューターが無限小数を有限桁で表現するために生じる誤差 | 円周率(3.14159…)を3.14と表現する | 計算結果のずれ、誤差の蓄積 | 計算桁数の増加、誤差を抑えるアルゴリズムの採用 |
身近に潜む打ち切り誤差の例

打ち切り誤差と聞くと、専門的な用語に聞こえ、自分たちの生活とは無縁に思えるかもしれません。しかし、実際には、打ち切り誤差は私たちの身近なところで影響を与えています。
例えば、毎日のように目にする天気予報を考えてみましょう。天気予報は、気温や気圧、風速など、様々な要素を基に、複雑な計算によって算出されています。しかし、これらの計算は、限られた時間の中ですべてを完全に計算することは不可能なため、ある程度のところで計算を打ち切っています。この打ち切られた部分が生む誤差が、天気予報の精度に影響を与える可能性があるのです。 つまり、私たちが普段目にする天気予報は、打ち切り誤差の影響を受けた、いわば「近似値」であると言えるでしょう。
また、コンピューターグラフィックスの世界でも、打ち切り誤差は重要な役割を果たしています。コンピューターグラフィックスでは、滑らかな曲線や複雑な形状を表現するために、無数の点と点を繋いで近似的に表現しています。この際、点と点の間隔を限りなく小さくすることで、滑らかな曲線に見せることができますが、実際には完全な曲線ではなく、微小な直線の集合体でしかありません。 この直線の集合体と本来の滑らかな曲線との間には、わずかながら誤差が存在し、これが打ち切り誤差の一種なのです。 このように、打ち切り誤差は、私たちの身の回りにある様々な場面で、その影響を及ぼしているのです。
| 例 | 説明 | 打ち切り誤差の影響 |
|---|---|---|
| 天気予報 | 気温や気圧などの要素を基に複雑な計算を行うが、計算時間には限りがあるため、ある程度のところで計算を打ち切る。 | 天気予報の精度に影響を与える可能性がある。 |
| コンピューターグラフィックス | 滑らかな曲線や複雑な形状を表現する際に、無数の点と点を繋いで近似的に表現する。点間の間隔を小さくすると滑らかに見えるが、実際は微小な直線の集合体である。 | 本来の滑らかな曲線との間に誤差が生じる。 |
打ち切り誤差への対策:精度と効率のバランス

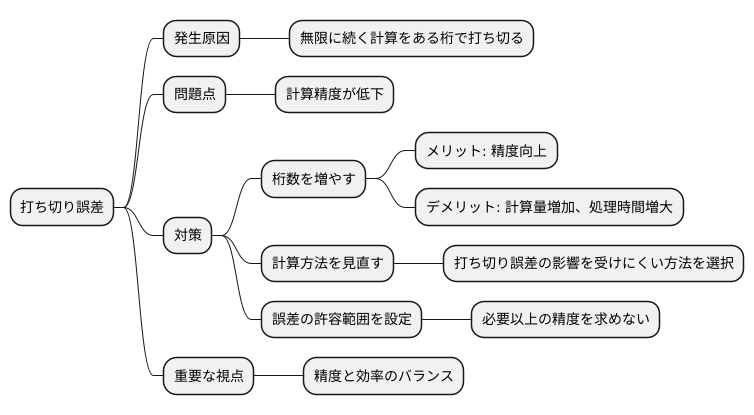
計算を行う上で、避けられない問題の一つに「打ち切り誤差」があります。これは、本来は無限に続く計算をある桁で打ち切ることで生じる誤差のことです。この誤差を完全に無くすことは不可能ですが、その影響を最小限に抑えるために、様々な対策が考えられています。
一つの方法としては、計算に用いる桁数を増やすことが挙げられます。桁数を増やすことで、より正確な値に近づくことができます。しかし、この方法には大きな欠点があります。それは、計算量が膨大になり、処理に時間がかかってしまうという点です。特に、大規模な計算や複雑な計算になればなるほど、この問題は顕著になります。
そこで重要になるのが、精度と効率のバランスです。時間ばかりがかかり、現実的な時間内に結果が得られなければ意味がありません。そこで、計算方法自体を見直したり、あらかじめ誤差の許容範囲を設定するなどの工夫が必要になります。
例えば、計算方法によっては、打ち切り誤差の影響を受けにくいものもあります。また、誤差の許容範囲をあらかじめ決めておくことで、必要以上の精度を求めることなく、効率的に計算を進めることができます。
このように、打ち切り誤差への対策は、単に精度を追求するのではなく、状況に応じて適切な方法を選択し、精度と効率のバランスを図ることが重要です。
更なる精度向上に向けて

計算機の性能向上は目覚ましく、以前には不可能だった複雑で大規模な計算が今では当たり前のように行われています。この進歩により、科学技術の様々な分野で飛躍的な進展が見られています。しかし、その一方で、数値計算に伴う誤差の問題は依然として課題として残っています。
計算機内部では数値は有限桁数で表現されるため、どうしても誤差が生じてしまいます。特に、無限に続く小数を有限桁数で表現する際に生じる「打ち切り誤差」は、計算結果に無視できない影響を与えることがあります。このような誤差は、計算を繰り返すことで蓄積し、最終的な結果に大きなズレが生じる可能性も孕んでいます。
誤差の影響を最小限に抑え、より正確な計算結果を得るためには、計算アルゴリズムの改善や計算機自体の進化が欠かせません。例えば、誤差の発生を抑えた新しい計算手法の開発や、より多くの桁数を扱える計算機の開発などが期待されています。
しかしながら、計算の仕組と誤差が発生する原理を理解し、適切に対処していくことが最も重要です。誤差の種類や発生源を把握し、状況に応じて適切な計算方法を選択したり、誤差の評価を行うことで、より信頼性の高い計算結果を得ることが可能になります。
| 計算機の性能向上と誤差問題 | 詳細 |
|---|---|
| 現状 | – 計算機の性能が飛躍的に向上 – 複雑で大規模な計算が容易に – 科学技術分野の進展に貢献 |
| 課題 | – 数値計算に伴う誤差の問題 – 特に「打ち切り誤差」の影響 – 計算の繰り返しによる誤差の蓄積 |
| 対策 | – 計算アルゴリズムの改善 – 計算機自体の進化 – 誤差の種類と発生源の理解 – 状況に応じた適切な計算方法の選択 – 誤差の評価による信頼性向上 |
