固定小数点数:コンピュータにおける数値表現の基礎

ITの初心者
先生、「固定小数点数」ってどういう意味ですか?コンピューターの中身の話みたいで、よくわからないです。

ITアドバイザー
そうですね。「固定小数点数」は、コンピューターが数を扱う方法の一つです。例えば、小数点以下2桁までしか使えない電卓があったとします。その電卓では「12.34」は表せますが、「12.345」は表せません。これが固定小数点数の考え方です。

ITの初心者
なるほど。でも、それじゃ表せる数が限られてしまいますね。コンピューターはもっと複雑な計算もできますよね?

ITアドバイザー
その通りです。固定小数点数は、表せる数の範囲は狭いですが、計算が速いというメリットがあります。そこで、より複雑な計算には「浮動小数点数」という方法も使われます。これは、小数点の位置を自由に変えられるため、より細かい数値を扱えます。
固定小数点数とは。
コンピューターで数を扱う方法の一つに「固定小数点数」というものがあります。これは、数の小数点の位置をあらかじめ決めておく方法です。整数部分と小数部分の桁数を決めておくことで、コンピューターは数を処理します。この方法は、決まった範囲の数を扱うことしかできませんが、計算速度が速いという利点があります。また、「固定小数点形式」と呼ばれることもあります。
数値表現の必要性

– 数値表現の必要性
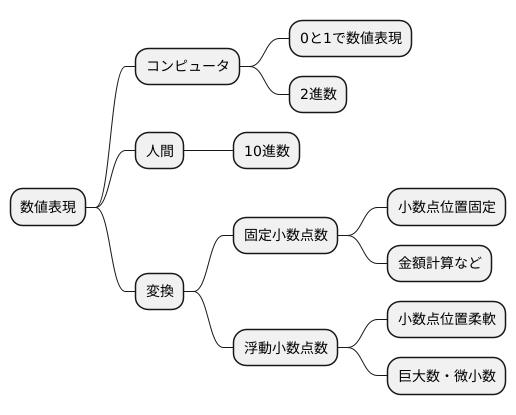
コンピュータは、計算やデータ処理を行う上で数値を欠かすことができません。しかし、コンピュータ内部では、数値は0と1の二つの記号の組み合わせで表現されます。これは、電圧の高低や電流の有無といった二つの状態を0と1に対応させているためです。
私たち人間は、普段10種類の数字を用いる10進数を使って数を表現しています。一方、コンピュータ内部で用いられるのは、0と1の二つの記号で数を表す2進数です。このため、コンピュータに計算をさせるためには、私たちが普段使っている10進数の数値を、コンピュータが理解できる2進数に変換する必要があります。
この10進数を2進数に変換する方法には、大きく分けて固定小数点数と浮動小数点数の二つがあります。固定小数点数は、小数点の位置を固定して数を表す方法です。これは、主に金額計算など、小数点以下の桁数が決まっている場合に用いられます。一方、浮動小数点数は、小数点の位置を柔軟に変えて数を表す方法です。これは、非常に大きな数や小さな数を扱う場合や、計算結果の精度を保つ必要がある場合に有効です。
固定小数点数の仕組み

– 固定小数点数の仕組み固定小数点数とは、数値の小数点の位置を特定の場所に固定して表現する方法です。 日常的に人間が使用する数値は、自由に小数点の位置を変えられる「浮動小数点数」で処理されることが多いですが、コンピュータ内部では、計算処理を簡略化するために固定小数点数が用いられることがあります。例えば、小数点以下2桁まで表現する場合を考えてみましょう。12.34という数値は、固定小数点数では内部的に1234という整数値として扱われます。これは、あらかじめ小数点の位置を「二桁右」と決めておくことで、整数値だけで小数を含む数値を表現できるという仕組みです。そして、この1234という整数値を100で割ることで、元の12.34という数値が得られます。固定小数点数は、このようにあらかじめ決められた桁数で整数部と小数部を表すことで、数値を表現します。この方法は、処理が単純で高速という利点があるため、計算資源が限られている組み込みシステムや、高速処理が必要な場面でよく使われています。
| 項目 | 説明 |
|---|---|
| 固定小数点数とは | 数値の小数点の位置を特定の場所に固定して表現する方法 |
| 仕組み | あらかじめ小数点の位置を決めておき、整数値だけで小数を表現する。例えば、小数点以下2桁まで表現する場合、12.34は内部的に1234という整数値として扱われる。 |
| 利点 | 処理が単純で高速 |
| 用途 | 計算資源が限られている組み込みシステムや、高速処理が必要な場面 |
固定小数点数のメリット

– 固定小数点数のメリット固定小数点数を使う一番の利点は、その処理速度の速さにあります。コンピュータ内部では、すべての数値は0と1の組み合わせで表現されます。この表現方法に従うと、小数を含む数値を扱う場合は、複雑な計算が必要になり、処理に時間がかかってしまいます。一方、固定小数点数は、小数点の位置をあらかじめ固定することで、あたかも整数のように扱うことができます。整数の計算はコンピュータにとって比較的単純な処理であるため、固定小数点数を使うことで、処理速度を大幅に向上させることが可能になります。この特性から、特に処理速度が重視される場面で固定小数点数は重宝されます。例えば、家電製品などに組み込まれて制御を行う組み込みシステムでは、限られた処理能力の中でリアルタイムな処理が求められるため、固定小数点がよく用いられます。また、ゲーム開発においても、キャラクターの動きや物理演算などを高速に処理するために、固定小数点が採用されることがあります。このように、固定小数点数は処理速度の面で大きなメリットを持つため、状況に応じて適切に使い分けることが重要です。
| メリット | 詳細 | 使用例 |
|---|---|---|
| 処理速度が速い | 小数点の位置を固定することで、整数と同様に処理できるため。 | – 組み込みシステム – ゲーム開発 |
固定小数点数のデメリット

– 固定小数点数のデメリット固定小数点数は、主に金額計算などの特定の用途でその威力を発揮しますが、一方で、いくつかのデメリットも抱えています。その中でも特に注意が必要なのが、表現できる数値の範囲が限られてしまうという点です。固定小数点数では、あらかじめ小数点以下の桁数が固定されているため、その範囲を超えてしまう大きな数値や、逆に非常に小さな数値を正確に扱うことができません。例えば、小数点以下2桁までに限定されている場合を考えてみましょう。この場合、100円25銭のように、小数点以下2桁までの金額は問題なく表現できます。しかし、10,000円を超えるような大きな金額や、0.01円未満の細かい金額を表現しようとすると、途端に限界に直面します。10,000円は小数点以下の桁数が足りずに正確に表せませんし、0.01円未満の金額は切り捨てられてしまうため、正確な計算ができません。このように、固定小数点数は、扱う数値の範囲があらかじめ予測できる場合に適していると言えます。逆に、扱う数値の範囲が広く、正確な計算が求められる場合には、固定小数点数ではなく、より広い範囲の数値を扱える浮動小数点数の利用を検討する必要があります。
| メリット | デメリット |
|---|---|
| 金額計算など、特定の用途で威力を発揮する | 表現できる数値の範囲が限られてしまう。 |
| 小数点以下の桁数が固定されているため、その範囲を超えてしまう大きな数値や、逆に非常に小さな数値を正確に扱うことができない。 | 扱う数値の範囲があらかじめ予測できる場合に適している。 |
| 扱う数値の範囲が広く、正確な計算が求められる場合には、浮動小数点数の利用を検討する必要がある。 |
浮動小数点数との比較

– 浮動小数点数との比較
数値を表す方法として、固定小数点数と並んで用いられるのが浮動小数点数です。固定小数点数が小数点の位置を固定して数値を表現するのに対し、浮動小数点数は小数点の位置を柔軟に移動させることができます。この柔軟性によって、浮動小数点数は非常に小さな値から非常に大きな値まで、広範囲な数値を表現することが可能です。
この特性から、浮動小数点数は、高い精度が求められる科学技術計算やシミュレーション、金融取引など、様々な分野で広く利用されています。例えば、宇宙空間における惑星の動きをシミュレーションする場合や、原子レベルの微細な現象を解析する場合など、非常に大きな値や小さな値を扱う必要がある場面において、浮動小数点数はその真価を発揮します。
しかし、浮動小数点数は、その複雑な構造ゆえに、固定小数点数と比較して処理速度が遅くなる傾向があります。これは、コンピュータが浮動小数点数を処理する際に、より複雑な計算を必要とするためです。そのため、処理速度が重視されるシステムにおいては、処理速度と精度のバランスを考慮して、固定小数点数と浮動小数点数のどちらを使用するかを決定する必要があります。
| 項目 | 固定小数点数 | 浮動小数点数 |
|---|---|---|
| 小数点の位置 | 固定 | 可変 |
| 表現できる数値範囲 | 狭い | 広い |
| 精度 | 低い | 高い |
| 処理速度 | 速い | 遅い |
| 用途 | 処理速度が求められるシステム | 高い精度が求められる計算 |
まとめ

– まとめ
コンピュータにおける数値表現には、主に固定小数点数と浮動小数点数の二つの方法があります。
固定小数点数は、小数点を固定して数値を表現する方法です。この方法は、計算が単純で処理速度が速いという利点があります。しかし、表現できる数値の範囲が狭く、大きな数値や非常に小さな数値を扱うことができません。そのため、速度が求められる一方で、扱う数値の範囲が限定的な場合に適しています。
一方、浮動小数点数は、小数点の位置を自由に移動させることで、広範囲な数値を表現する方法です。この方法は、固定小数点数では表現できないような大きな数値や小さな数値を扱うことができます。しかし、計算が複雑になるため、処理速度が遅くなるという欠点があります。そのため、処理速度よりも、広範囲な数値を正確に表現することが求められる場合に適しています。
どちらの数値表現方法を選択するかは、アプリケーションの目的や要件によって異なります。例えば、高速な処理が求められるゲーム開発などでは固定小数点数が、高い精度が求められる科学技術計算などでは浮動小数点数が用いられることが多いです。
| 項目 | 固定小数点数 | 浮動小数点数 |
|---|---|---|
| 特徴 | 小数点の位置を固定 | 小数点の位置を自由に移動可能 |
| メリット | – 計算が単純 – 処理速度が速い |
– 広範囲な数値を表現可能 |
| デメリット | – 表現できる数値の範囲が狭い – 大きな数値や非常に小さな数値を扱うことができない |
– 計算が複雑 – 処理速度が遅い |
| 用途例 | – 速度が求められるゲーム開発 | – 高い精度が求められる科学技術計算 |
